编译原理总结与复习

[TOC]

文法到字符称为推导
字符到文法称为归约
那么最右推导称为规范推导，最左归约称为规范归约

编译过程

词法分析的任务：输入源程序，对构成源程序的字符串进行扫描和分解，识别出一个个的单词
语法分析的任务是：在词法分析的基础上，根据语言的语法规则，把单词符号串分解成各类语法单位（语法范畴），如“短语”、“子句”、“句子”（“语句”）、“程序段”和“程序”等。通过语法分析，确定整个输入串是否构成语法上正确的“程序”
语义分析与中间代码产生:对语法分析所识别出的各类语法范畴，分析其含义，并进行初步翻译（产生中间代码）
优化:对产生的中间代码进行加工变换，以期在最后阶段能产生出更为高效（省时间和空间）的目标代码
目标代码生成:把中间代码（或经优化处理之后）变换成特定机器上的低级语言代码。
表格处理和出错处理

文法与语言

语言是由句子组成的集合，或说是由一组符号串所构成的集合。

文法是对语言结构的定义与描述。即从形式上用于描述和规定语言结构的称为“文法”（或称为“语法”）
语法树：我们用语法树来描述一个句子的语法结构
文法的结构定义:

文法G=（VN，VT，P，Z）
   VN ：非终结符号集
   VT ：终结符号集
   P：产生式或规则的集合
   Z：开始符号（识别符号）  Z∈VN
产生式：产生式是一个有序对(U, x), 通常写为:
 U :: x 或U  x；      | U|  1 ,  |x|  0
②非终结符号：出现在产生式的左部,且能推出符号或符号串的那些符号。其全体构成非终结符号集，记为VN 。
③终结符号：不出现在产生式的左部,且不能推出符号或符号串的那些符号。其全体构成终结符号集，记为VT

最右推导：若符号串α中有两个以上的非终结符时，对推导的每一步坚持把α中的最右非终结符进行替换，称为最右推导。
最左推导：若符号串α中有两个以上的非终结符时，对推导的每一步坚持把α中的最左非终结符进行替换，称为最左推导。
递归文法: if U=+=>…U… 递归文法; U=+=>U…… 左递归文法;U=+=>…U右递归
递归产生式: U=xUy 若x=ε即U=Uy 左递归;U=xU 右递归
左递归不能用自顶向下进行语法分析
递归文法可用有穷条产生式,定义无穷语言

左递归转换为右递归

消除直接左递归:引入新的变量A’
消除间接左递归:先用间接左递归文法转换为直接左递归,然后用1的直接消除

文法分类

狗逼乔姆斯在1956年建立形式语言的描述,并将文法和语言分为 0型,1型,2型,3型;
– 0型: u::=v; (u∈V* ，v∈V)称为短语结构文法.,产生式左右都是符号串,L0这种语言图灵机可以接受;
– 1型: xUy::= xuy;(U∈VN， x、y、u∈V) 称为上下文敏感或上下文有关文法,L1可以由一种线性界限自动机接受
– 2型: U::= u( U∈VN， u∈V*); 称为上下文无关文法CFG;L2可以由下推自动机接受
– 3型: P: U::=t或U::=Wt(U,W∈VN t∈VT);称为正则文法RG,可以由有穷自动机接受

经常使用2型文法:原因如下:

2型文法拥有足够强的表达能力来表达大多数的程序设计语言,几乎所有的语言都是通过上下文无关文法来定义的
上下文无关文法足够简单,可以构造有效的分析算法来检验一个给定的字符串是否由某个上下文无关文法产生,如LR分析器和LL分析器,

语法树与二义性文法

语法树: 句子结构的图示表示法,它是一个有向图,有结点和有向边组成;

文法二义性:若对于一个文法的某个句子存在两颗不同的语法树,文法是二义性文法,否则则不;

编译原理的词法分析

单词的描述工具,单词的识别系统,设计和实现词法分析程序:描述和刻画程序设计语言的单位–单词,然后识别单词的相关动作,

__正则表达式,设别机制,和有穷状态自动机;

词法分析是编译过程中的第一个阶段，在语法分析前进行；也可以和语法分析结合在一起作为一遍，由语法分析程序调用词法分析程序来获得当前单词供语法分析使用.
从语法分析独立出来的原因就是:

1简化设计–编译过程的大部分时间都是花费在扫描字符上.
2改进编译效率–单词的词法规则很简单,可以建立特别适合用于这种词法规则的有效技术,实现词法分析的自动生成,
3增加编译系统的可移植性– 词法分析作为一个独立的子程序,供语法分析程序调用(想改就改这一部分的)

单词一般分为五类: 关键字,标识符,常数,运算符,界限符

词法分析器设计

输入,预处理:输入放入缓冲区内;预处理将某些跳格符,回车符和换行等编辑性字符,没有意义,可以剔除.注解部分预处理是也要剔除,空白符(空格符)把多个结合成一个
单词符号的识别:超前搜索
词法分析器对当前扫描缓冲区进行扫描时一般是使用两个指示器,一个指向当前正在识别的单词的开始位置(首字符),另一个用于向前搜索以找到单词的终点,无论扫描缓冲区设置多大,都不能保证单词符号不会越界,因此扫描缓冲区一般设置一分为二的区域;
正则表达式:| . *符号

要满足以下条件仅由有限次使用上述三步骤而定义的表达式才是上的正规式，仅由这些正规式所表示的集合才是上的正规集
- 正则式和正规集的转换
- 若两个正规式e1和e2所表示的正规集相同,则说e1和e2等价,写成e1=e2 e1= b(ab)* , e2 =(ba)*b，那么e1= e2
- U,V,W为正规式，正规式服从的代数规律有
有穷自动机:作为一种识别装置，它能准确地识别正规集，即识别正规文法所定义的语言和正规式所表示的集合.分为两类:确定的有穷自动机(DFA)\不确定的有穷自动机(NFA)
- DFA定义:一个确定的有穷自动机M是个五元组M=（K，Σ，f，s0 ，Z）1) k是有穷状态集合,∑是字母表,f是转换函数,s∈k 是一个初态,z∈k是一个终态可空.2) 可以使用状态转换矩阵表示,初态结点的旁边标以 =>；终态结点旁边标 —;3)可以表示成一张状态转换图的形式,是一张有限方向图( 一张转换图只包含有限个状态（即有限个结点），其中有一个被认为是初态用=>表示，而且实际上至少要有一个终态（用双圈表示）)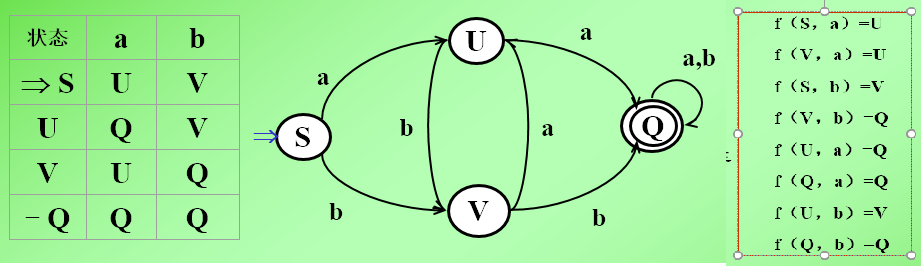
- DFA确定性:1)映射唯一:对任何状态s∈K和输入符号a∈Σ，f（s，a）唯一地确定了下一状态,任何一个状态结点最多只有n条弧射出，而且每条弧以一个不同的输入字符标记。2)DFA有且仅有唯一的一个初态s0∈K 。
- NFA定义:非确定的有穷自动机（NFA）M是一个五元组：M=（K，Σ，f，S ，Z）,有多个初态,状态多个;0表示非终态,1为终态行
- DFA与NFA区别:(1)DFA没有输入空串之上的转换动作；(2)对于DFA，一个特定的符号输入，有且只能得到一个状态，而NFA就有可能得到一个状态集。DFA只有唯一的初态，而NFA有可能有多个初态
NFA转DFA(NFA确定算法):DFA的每一个状态对应NFA的一组状态,转换函数的定义： d([S1 S2,... Sj],a)= [R1R2... Rt] 其中 {R1,R2,... , Rt} = ε-closure(move({S1, S2,,... Sj},a))
- ε - closure({集合})表示从集合里面经过任意条 € 到达的节点集合包含自身节点, mvoe({集合},a)集合里面的节点表示经过a到达的节点(不包含自身);记：Ia=ε-closure(J ) =ε-closure(move(I,a) )
DFA的化简:
最小状态DFA:1)没有多余状态,2)没有两个状态是互相等价的
正规式与有穷自动机的等价性:

NFA转DFA

状态集合I的ε-闭包，表示为ε-closure(I)，定义为一状态集，是状态集I中的任何状态S经任意条ε弧而能到达的状态的集合
状态集合I的a弧转换，表示为 J=move(I,a) ，定义为一状态集合J，J是所有那些可从I中的某一状态经过一条a弧而到达的状态的全体
Ia=ε-closure(J ) =ε-closure(move(I,a) )

没有多余状态(死状态)；
2.没有两个状态是互相等价（不可区别）

编译过程